Matematika Dasar untuk Machine Learning

Machine Learning (ML) bukan hanya tentang menulis kode dan menggunakan pustaka seperti Scikit-learn atau TensorFlow. Di balik algoritma yang digunakan, terdapat konsep matematika yang menjadi fondasinya. Memahami matematika dasar membantu kamu:
- Membaca paper dan dokumentasi dengan lebih mudah,
- Memahami “mengapa model bekerja seperti itu”, bukan hanya “bagaimana menggunakannya”,
- Menyusun solusi yang lebih optimal dan interpretatif.
Berikut adalah empat topik matematika inti yang perlu dikuasai untuk belajar Machine Learning.
Aljabar Linear: Vektor, Matriks, dan Operasi Dasar
Machine Learning bekerja dengan data numerik yang sering diwakili dalam bentuk vektor dan matriks.
Vektor
Vektor adalah array satu dimensi. Contohnya, fitur dari sebuah data bisa ditulis sebagai:

Misalnya, data rumah:
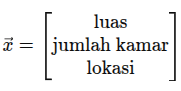
Matriks
Matriks adalah array dua dimensi, sering digunakan untuk menyimpan banyak data sekaligus:
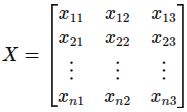
Operasi Dasar
- Penjumlahan/Pengurangan vektor dan matriks
- Perkalian skalar dan dot product
- Perkalian matriks
- Transpos (AT), invers (A-1), determinan
Kegunaan dalam ML
- Persamaan regresi linear: y= Xw + b
- Optimisasi dan update bobot dalam neural networks
- Transformasi ruang (PCA, rotasi, scaling)
Kalkulus: Turunan, Gradien, dan Optimisasi
Turunan (Derivative)
Turunan menunjukkan bagaimana suatu fungsi berubah. Dalam ML, ini digunakan untuk:
- Menentukan arah perubahan fungsi loss
- Menghitung sensitivitas prediksi terhadap input
Contoh: turunan fungsi error terhadap parameter model.
Gradien
Gradien adalah vektor turunan parsial dari fungsi multivariabel. Dalam konteks model ML, gradien menunjukkan arah tercepat untuk meminimalkan kesalahan (loss):
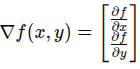
Optimisasi
Optimisasi adalah proses menemukan parameter terbaik yang meminimalkan fungsi loss. Contohnya:
- Gradient Descent adalah algoritma yang menggunakan gradien untuk memperbarui parameter:
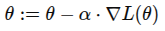
Kegunaan dalam ML
- Training model melalui backpropagation
- Fine-tuning hyperparameter
- Loss minimization
Statistika & Probabilitas
Statistika dan probabilitas penting untuk memahami data dan membuat prediksi.
Ukuran Pemusatan dan Penyebaran
- Mean (rata-rata):
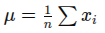
- Variance:
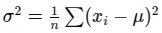
- Standard Deviation: akar dari variance
Distribusi Probabilitas
- Distribusi Normal (Gaussian): umum digunakan untuk model linear, noise, dan prior dalam Bayesian.
- Distribusi Binomial, Poisson, Bernoulli: penting dalam klasifikasi dan NLP.
Teorema Bayes
Bayes digunakan dalam probabilistik inference:
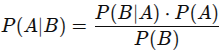
Contoh penggunaannya adalah di model Naive Bayes classifier.
Kegunaan dalam ML
- Inferensi statistik dan prediksi
- Mengukur ketidakpastian
- Membangun model probabilistik
Notasi dan Simbol Umum dalam Machine Learning
| Simbol | Arti |
|---|---|
| Input data | |
| Target/output | |
| Prediksi dari model | |
| Parameter model | |
| Loss function | |
| Gradien | |
| Penjumlahan dan perkalian | |
| Ekspektasi dari variabel acak xx | |
| Fungsi sigmoid | |
| arg min, arg max | Nilai input yang meminimalkan/memaksimalkan fungsi |
Penutup
Memahami matematika di balik Machine Learning bukan sekadar untuk keperluan akademik. Ia membentuk intuisi yang dalam, membantu debugging model, dan membuatmu mampu membangun solusi dari dasar. Tidak harus menjadi ahli matematika, tetapi memahami konsep intinya akan membuat kamu lebih percaya diri dalam membangun sistem yang cerdas.





